最近前端一直被Vue折腾,算法一直被CNN折腾,倒是后端相安无事。毕竟SpringBoot都学完了,我在本科阶段的Java开发暂时取得了一些成绩,说的不好听就是找不到方向了,到了瓶颈。
昨天晚上(2022.3.18)被ElementUI Plus烦透了,于是捧起书看看机器学习的算法。非常遗憾,我在这方面的知识积累还是非常有限的,应该把重心从工程调整到机器学习了,前端打算暂时放一放。
恰好有一门课的老师要求讲一讲算法,因为我之前在图像处理方面有过一些发展,所以我还是选择讲这个方面的东西。不过要把一个算法真正讲懂,这可不是一件容易的事情,因为会用一个算法,和理解一个算法,这是毫不相干的事情。
这篇前缀有点长了,好吧,不管话有没有说完,全部省略,反正我打算讲k-近邻算法。这篇算法的讲解参考Peter Harrington所著的《Machine Learning in Action》,当然会融入我的一些思考。我之所以讲这个算法,第一是因为这个算法当作一个机器学习入门十分合适,第二是因为,这可能是花最短时间,能给最多人讲懂的算法了。
首先我们做一个假设。如果有一群成年人和婴儿,我们应该如何将其快速区分呢?答案多种多样,我在这里选择两个指标:身高和体重。有了这两个指标,我们非常容易的就可以将成年人与婴儿区分开,因为这两个群体在这两个指标上,都有着非常明显的差异。
那我们如何使用计算机,通过这两个指标来做一个简单的二分类呢?也许一个if-else语句就可以搞定,这是一个聪明的做法,但不要来砸场子,我们在这里,引入k-近邻算法。
我们假设已经有了一堆成年人与婴儿的身高和体重数据,当然作为训练集,这些数据都已经提前设置好了标签。当我们输入一个没有标签的数据后,我们会将新数据的身高和体重与训练集中的每个数据进行比较,然后提取出训练集中,特征最为相似的分类标签(即判断是成年人还是婴儿)。我们一般选择前k个最为相似的数据,作为最终的结果。这就是k-近邻这个名字的由来。
好了,我已经把这个算法的基本思想讲了一遍。也许没听懂,有疑问的地方可能是,我们如何进行比较呢?既然是选择最邻近的,那我们日常生活中,如何衡量邻近呢,那就是距离!
我们引入一个大家都知道的公式:
$$d=\sqrt{(xA_{0}-xB_{0})^{2}+(xA_{1}-xB_{1})^{2}}$$
不多解释了,举个例子吧。
例如我们有一个未知数据。体重78kg,身高1.75m,我们来把他交给计算机,判断是成人还是婴儿。首先我们写成向量的形式,就是:
$$\left[ 78,1.75\right]$$
假设我们计算机内,已经有一些含有标签的数据了。大概像这样:
$$[5,0.6],[4,0.55],[4.3,0.54],[4.1,0.55],[4.8,0.56]$$
$$[70,1.75],[65,1.71],[67,1.76],[75,1.78],[80,1.84]$$
前者是婴儿的数据,后者就是成年人的数据。
我们就把这些向量当作点的坐标,绘制在同一张坐标系上试试吧。
我们使用Python的matplotlib库进行绘制,代码如下:
import matplotlib.pyplot as plt
import numpy
from numpy import *
datingDataMat = [[5, 0.6], [4, 0.55], [4.3, 0.54], [4.1, 0.55], [4.8, 0.56], [70, 1.75], [65, 1.71], [67, 1.76],
[75, 1.78], [80, 1.84]]
datingLabels = [1, 1, 1, 1, 1, 2, 2, 2, 2, 2]
datingDataMat=numpy.array(datingDataMat)
datingLabels=numpy.array(datingLabels)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(datingDataMat[:, 0], datingDataMat[:, 1], 15.0 * array(datingLabels), 15.0 * array(datingLabels))
plt.show()绘图结果如下:
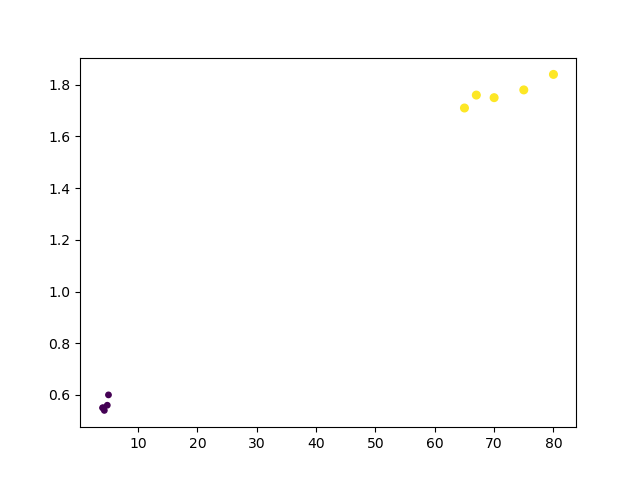
在这里,紫色代表婴儿,黄色代表成年人。我们可以很明显的看出来,紫色和黄色的点距离都十分接近,这就刻画出我们所说的“近邻”。
如果我们把未知数据放到这张图上,一定会跟紫色的点非常邻近,我们刻画这种距离的方式就是最简单的,两点间距离公式。我们将未知数据与训练样本集中的数据求距离,再通过排序算法,选出前k个最邻近的样本,前k个样本的标签就是我们需要的分类依据。当然,如果前k个样本的标签不一致,我们就拿最粗暴的解决方式,谁出现的次数最多,就是谁。不过我们得给他一个好听的名字:多数投票法。
好了,我们看完这个简单的二分类,应该开始进入我们的主题了:图像识别。但先不要急,我们再介绍一个小东西。
我们在上一个案例中,选取身高和体重两个指标进行分类,但其实如果我们按部就班,就会发现身高这个指标对距离几乎没有影响。因为这个身高和体重这两个数字指标差距实在太大了。身高特征会在求距离的过程中,被体重指标给抹去影响。那我们有没有办法解决呢?把身高的单位换成厘米?这显然不是一个好办法。
我们在这里引入归一化这个概念。其实这个概念在Java课程的时候,老师就有提过,不过是以另一种方式,不涉及具体的算法。归一化,就是将让所有的指标,都落在0和1之间,这样,身高和体重的影响就被平均了,这是个好办法。直接上现成的公式:
$$X_{n}=\frac{X-X_{min}}{X_{max}-X_{min}}$$
这样我们的数据就可以落到0和1之间了。
好了,最后一个问题解决了,我们来看图像识别。
我们还是不讲很复杂的图像识别,但是不再是二分类问题了,这是一个多分类的问题。我们需要识别手写数字。至于这个图像如何转换成我们需要的数据,很简单,看一张图就明白了。

我们在这里仅将其转为0和1两种数值,当然你要是有兴趣也可以用标准的RGB通道将其转为255数值。是否归一化其实在这里不是很重要了。
解决了图片转换的问题,那我们就按照之前的思路,用k-近邻算法来实现简单的鉴别吧。只不过我们这里的点不再是存在于二维的了,不过这不影响我们使用算法,只不过我没办法形象的描述了。所以我们直接上案例吧。
首先我们放出测试集和训练集,这些都是《Machine Learning in Action》的作者提供的,十分感谢。
还有一些代码:
from os import listdir
from numpy import *
import operator
#分类算法
def classify0(inX, dataSet, labels, k):
dataSetSize = dataSet.shape[0]
diffMat = tile(inX, (dataSetSize, 1)) - dataSet
sqDiffMat = diffMat ** 2
sqDistances = sqDiffMat.sum(axis=1)
distances = sqDistances ** 0.5
sortedDistIndicies = distances.argsort()
classCount = {}
for i in range(k):
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
#将文件转为矩阵
def file2matrix(filename):
fr = open(filename)
numberOfLines = len(fr.readlines())
returnMat = zeros((numberOfLines, 3))
classLabelVector = []
fr = open(filename)
index = 0
for line in fr.readlines():
line = line.strip()
listFromLine = line.split('\t')
returnMat[index, :] = listFromLine[0:3]
classLabelVector.append(int(listFromLine[-1]))
index += 1
return returnMat, classLabelVector
def img2vector(filename):
returnVect = zeros((1,1024))
fr = open(filename)
for i in range(32):
lineStr = fr.readline()
for j in range(32):
returnVect[0,32*i+j] = int(lineStr[j])
return returnVect
#算法测试
def handwritingClassTest():
hwLabels = []
trainingFileList = listdir('trainingDigits')
m = len(trainingFileList)
trainingMat = zeros((m,1024))
for i in range(m):
fileNameStr = trainingFileList[i]
fileStr = fileNameStr.split('.')[0]
classNumStr = int(fileStr.split('_')[0])
hwLabels.append(classNumStr)
trainingMat[i,:] = img2vector('trainingDigits/%s' % fileNameStr)
testFileList = listdir('testDigits')
errorCount = 0.0
mTest = len(testFileList)
for i in range(mTest):
fileNameStr = testFileList[i]
fileStr = fileNameStr.split('.')[0]
classNumStr = int(fileStr.split('_')[0])
vectorUnderTest = img2vector('testDigits/%s' % fileNameStr)
classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)
print("算法返回: %d, 真实值: %d" % (classifierResult, classNumStr))
if (classifierResult != classNumStr): errorCount += 1.0
print("\n总错误数: %d" % errorCount)
print("\n总错误率: %f" % (errorCount/float(mTest)))剩下的只能自己去研究了。
这篇文章主要用于我上课讲述,所以会有很多内容是我现场补充的,等我的课上完了,我再回来补充到文章里。

为啥要在shanwer的博客发
之前就在这里发过东西呀,主要是自己的博客挂在树莓派上,指不定什么时候就一命呜呼了。而且咱发的东西质量也不会很差。
咱们老hxd了√
彳亍